Mplus7.0潜类别分析（Latent Class Analysis, LCA）零基础教程

0 序言

最近小白分析数据用到了潜类别分析（Latent Class Analysis，LCA），它通常用于多组二分类数据的分类（或聚类），主要适用于变量都是二分类变量的情况。

LCA的应用，举例来说，我们可以通过数个新冠应对行为（戴口罩、勤洗手、居家隔离、大量消毒、预防性服药等）将10000+名公众的应对习惯归类为戒备型、冷静型、无畏型[1]。

这篇博文中，小白以Mplus7.0介绍LCA的大体分析流程。第一部分展示LCA分析的主要内容，看看数据文件样式，简单了解指标判断，让大家有个大体的概念；第二部分以小白正在进行的一个行为健康的研究为示例，结合数据分析，介绍一遍开展LCA的过程，力求做到零基础也能掌握LCA。

1 LCA分析的主要内容

进行LCA分为两个步骤。一是通过模型比较选分类模型，通过指标判断选定将样本分为N类，见1.1部分。二是确定分为N类后，基于N分类模型中条件概率对结果进行定义，见1.2部分。

1.1选择分类模型

第一步比较分类模型，基于AIC，BIC，VLMR-LRT，BLRT，Entropy，类别概率等指标。下图所示展示了文献[2]的模型比较示例，通过模型比较，选定7分类模型（N=7），即可将样本聚为7类。

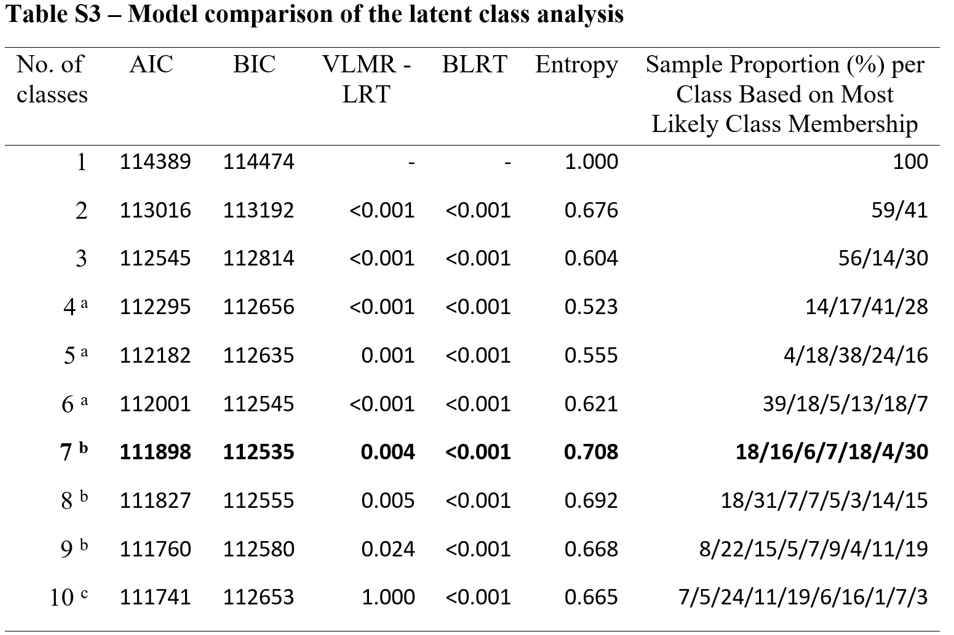
来源：文献[2]。

1.2 分类定义

第二步，通过条件概率对各分类进行定义。如下图展示文献[3]的分类结果与定义。虚线所代表的聚类在physical inactivity上概率接近1.00，在obesity上概率约0.43，在smoking上的概率约为0.22，在risky drinking上约为0.20，在physical inactivity与obesity上的特征相对突出，因而作者将其定义为Inactive-and-obese class。点线所代表的聚类在physical inactivity上概率接约0.41，在obesity上概率约0.11，在smoking上的概率接近1.00，在risky drinking上约为0.81，在smoking与risky drinking上的特征相对突出，因而作者将其定义为Smoking-and-risky-drinking class。

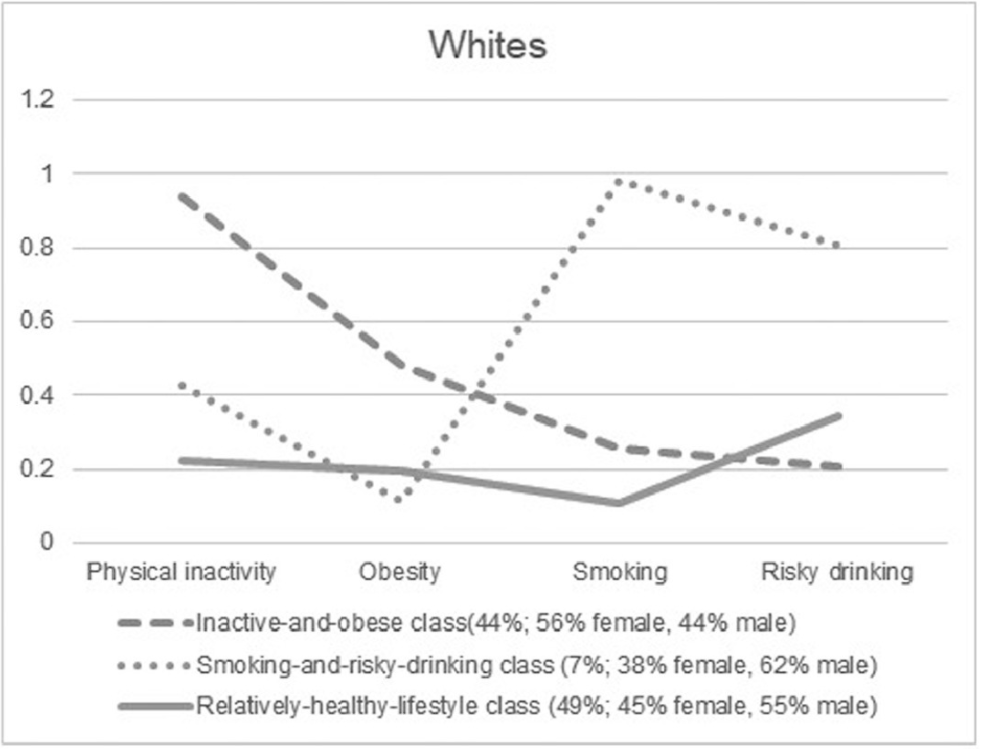
来源：文献[3]。

2 指标判断

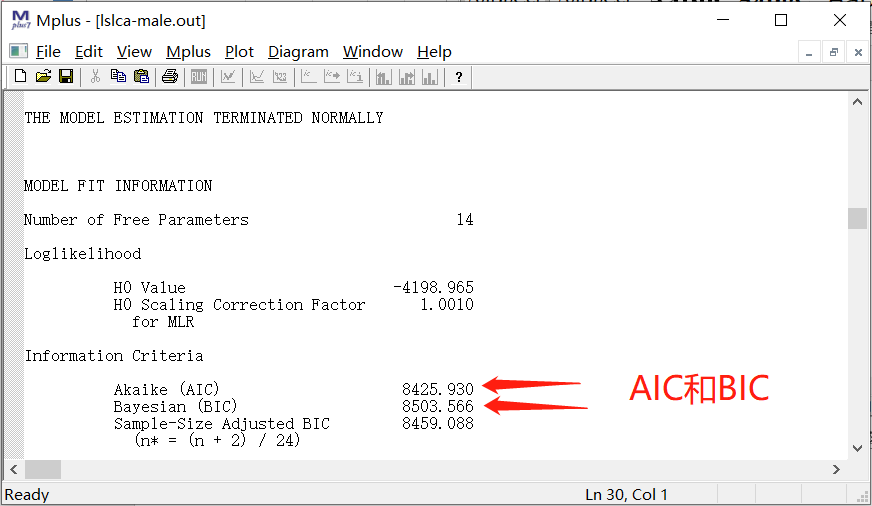
1.AIC (Akaike information criterion)，越小越好。
2.BIC（Bayesian information criterion），越小越好。
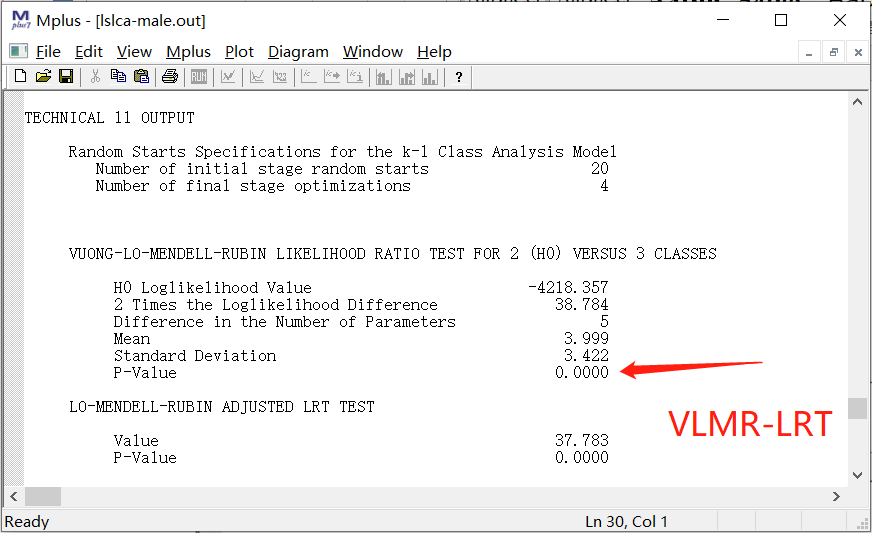
3.VLMR-LRT (Vuong-lo-mendell-rubin likelihood ratio test)，看P值，当P小于0.05，说明当前模型优于n-1模型。
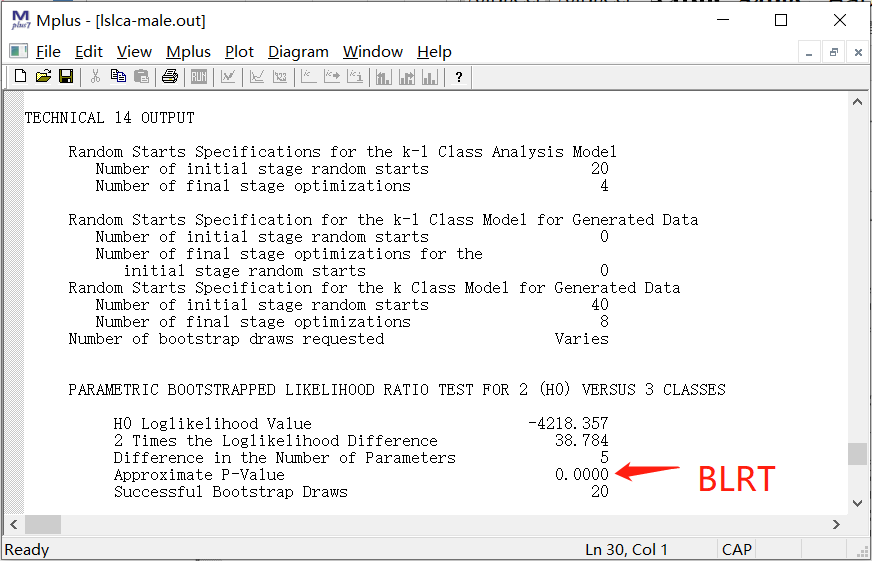
4.BLRT (bootstrap likelihood ratio test)，看P值，当P小于0.05，说明当前模型优于n-1模型。
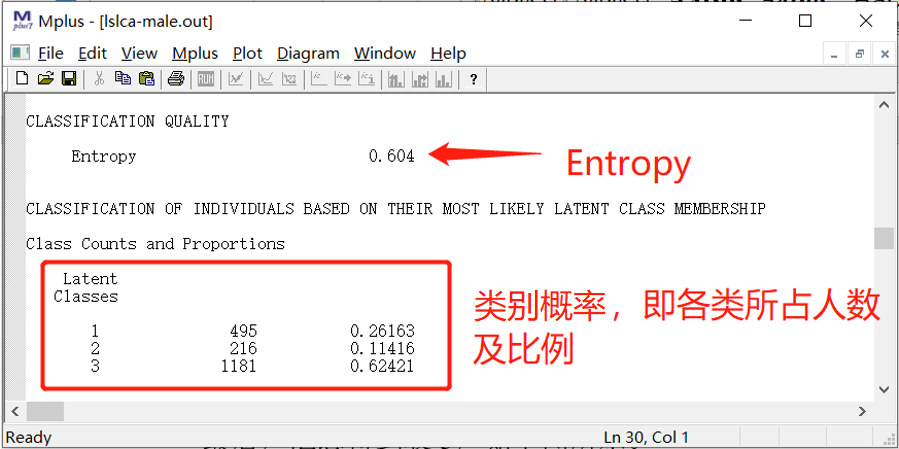
5.Entropy，表示分类正确的概率，越高越好。
6.类别概率，即各个类别的占比，主要看类别概率分布是否均衡，不存在单类占比特别低的情况（若存在，最好有事实依据）。

3 数据文件样式

由于涉及到潜变量的分析，本例以Mplus7.0为主要软件开展。

Mplus通常使用的数据为dta或txt格式的数据，这里我们使用dat数据。注意，数据文件和Mplus的inp文件放到同一文件架内。

小白主要使用两种方式可以保存Mplus需要的数据格式：
1）通过N2MPLUS的转化软件。转为可被Mplus分析的dat数据文件。N2MPLUS由Daniel S. Soper开发并提供下载。
2）excel另存为txt。注意txt中不包含首行概念信息，excel另存为txt的需要手动删掉第一行。

接下来，小白对根据抽烟、酗酒、不运动、失眠等四个危险健康行为数据，样本中的男性进行LCA分析，可以看到，失眠（slp），不运动（exr），抽烟（smk），酗酒（alc）均为二分类数据，0表示无该行为，1表示有该行为。数据在SPSS中的形式如下图所示：

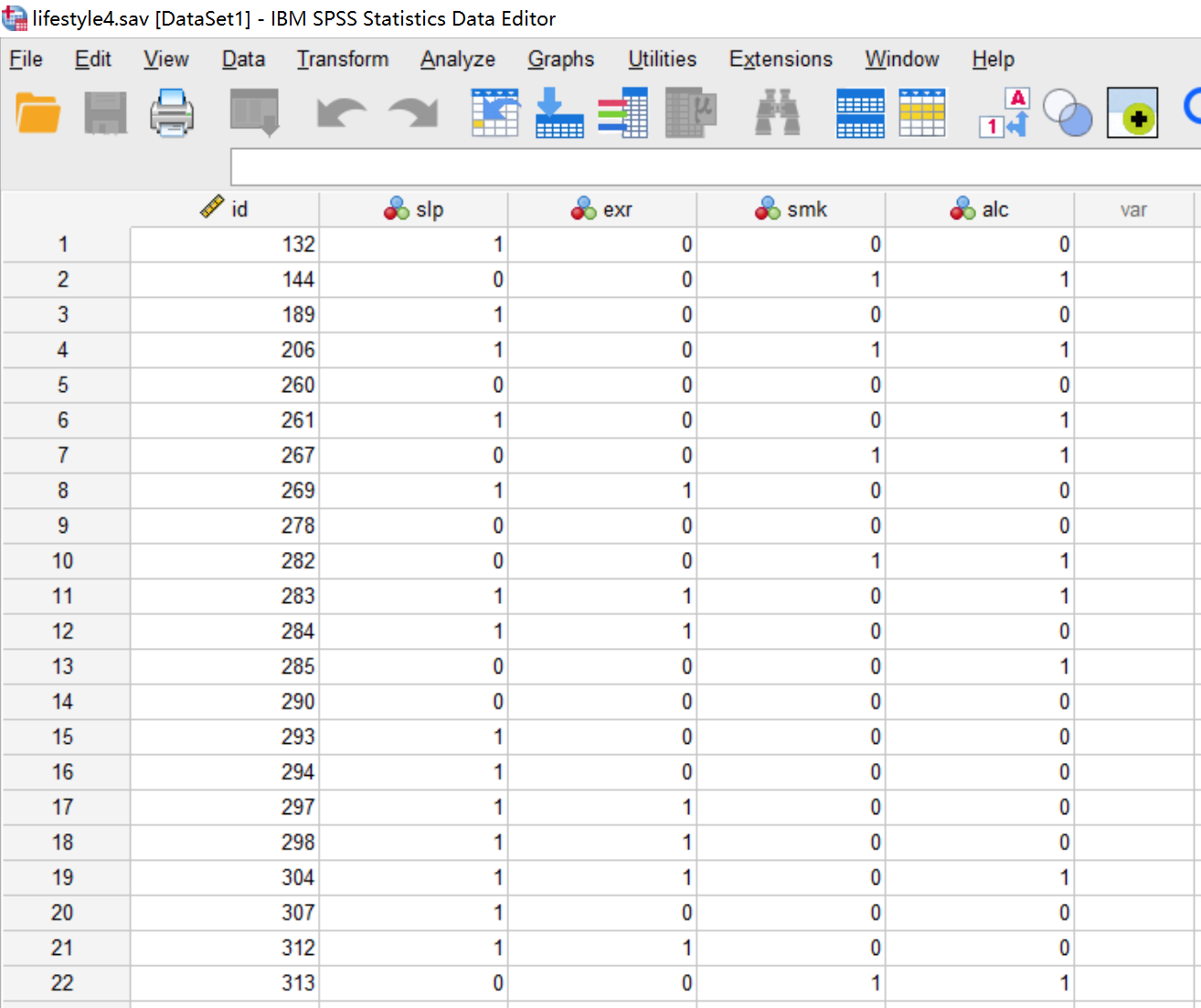
4 数据分析

4.1 模型构建

从1分类模型开始，2类、3类、4类……，构建多个潜类别模型。通过classes参数的设定，将slp，exr，smk，alc等数据聚为1类，代码如下：

DATA: FILE IS lifestyle4.dat;

VARIABLE: NAMES ARE id smk alc ecr slp;
          USEVARIABLES ARE smk alc ecr slp;
          CATEGORICAL = smk alc ecr slp; ! 定义分类变量
          CLASSES = c(1); !设定分为1类

ANALYSIS:TYPE = MIXTURE;

OUTPUT: 
       TECH11 TECH14;

变化classes参数，聚为2类，代码如下：

DATA: FILE IS lifestyle4.dat;

VARIABLE: NAMES ARE id smk alc ecr slp;
          USEVARIABLES ARE smk alc ecr slp;
          CATEGORICAL = smk alc ecr slp; ! 定义分类变量
          CLASSES = c(2); !设定分为2类

ANALYSIS:TYPE = MIXTURE;

OUTPUT: 
       TECH11 TECH14;

4.2 分析结果

记录每一次模型的结果，以下以3分类模型为例，汇总结果数据。以下，我们找到AIC，BIC，VLMR-LRT，BLRT，Entropy，类别概率等指标。

4.2.1 AIC和BIC

4.2.2 VLMR-LRT

4.2.3 BLRT

4.2.4 Entropy与类别概率

4.2.5模型比较的结果汇总

最后，汇总得到下表。

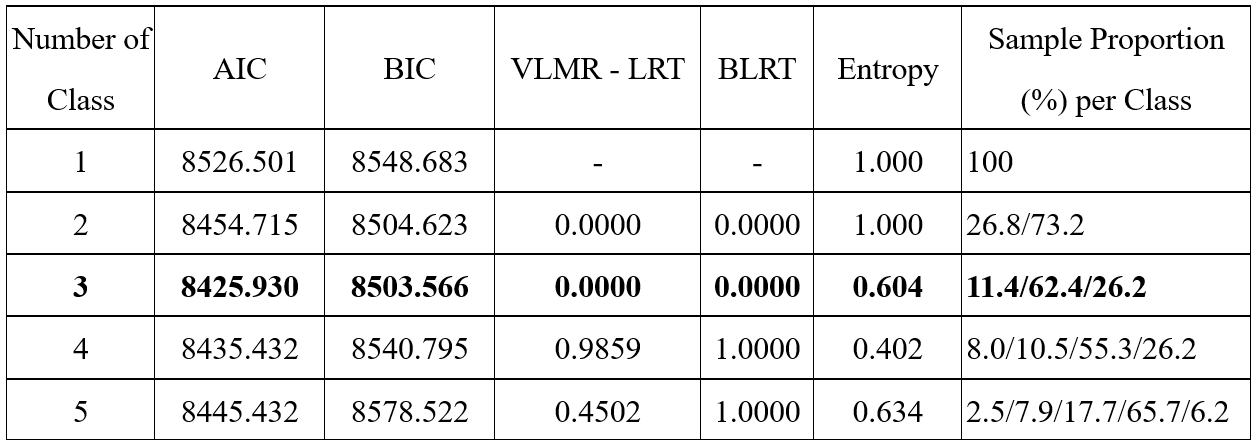
上述指标中，从AIC和BIC看，3分类最小；3分类的VLMR-LRT和BLRT的P值均小于0.05，表明3分类模型显著优于2分类模型，而4分类模型的P值均大于0.05，表明4分类模型不显著优于3分类模型；Entropy中高于0.6的有3分类和5分类；从各分类占比看，2分类-4分类模型中的分布均匀，5分类中有一类占比仅为2.5%人。综合各类指标判断，选定3分类模型。进一步输出3分类模型的各分类概率，见4.2.6部分。

4.2.6 条件概率分布

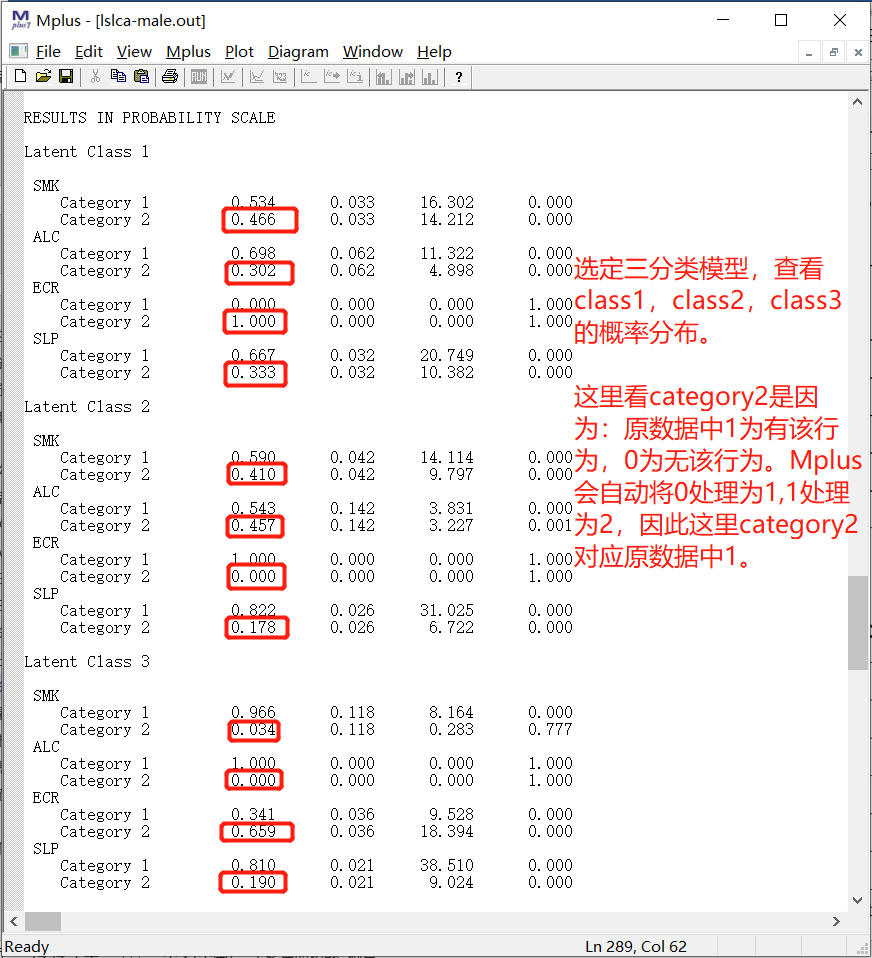
4.2.7 条件概率与定义

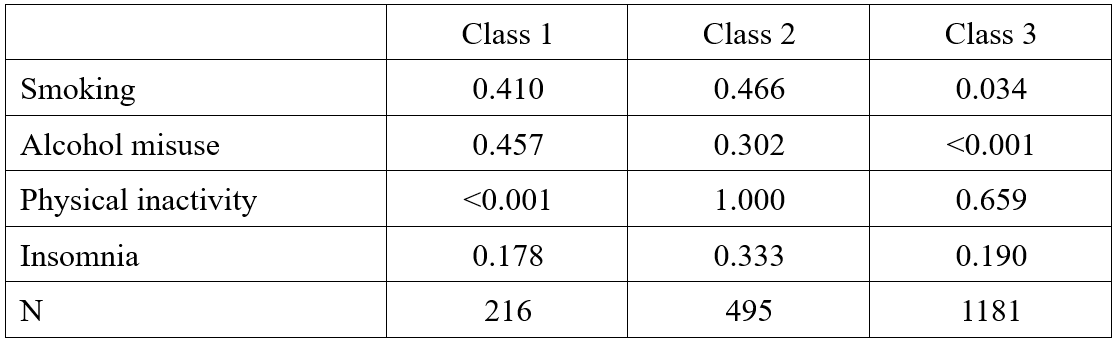
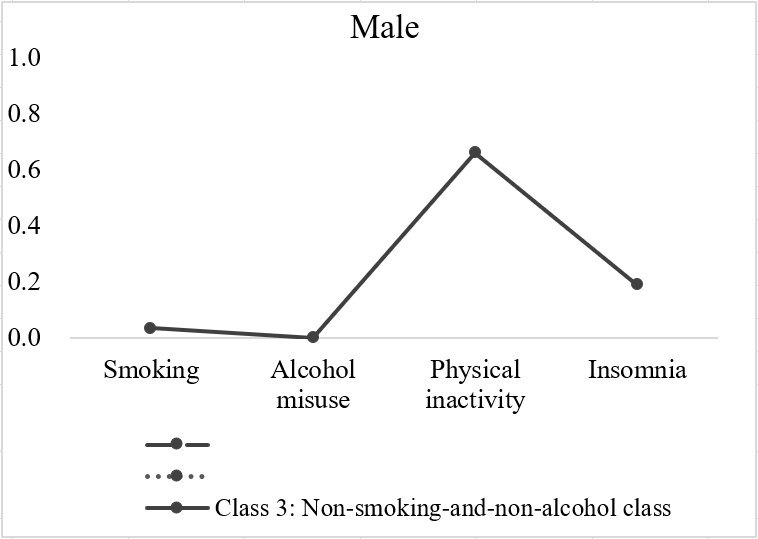
根据条件概率，小白以class3为例画图，更清晰理解class3男性的特征，如下：
相较于其他两类，class3这类男性的主要特征是不抽烟、不酗酒，可以归为Nonsmoking-and-non-alcohol class一类。

5 保存聚类结果

选定3分类后，我们希望知道，每个人分别被分到哪一类。通过以下SAVEDATA的两句命令，将聚类的结果保存下来，为其他分析做基础（例如我们希望知道每个聚类的人群的基本特征）。

DATA: FILE IS lifestyle.dat;

VARIABLE: NAMES ARE id smk alc ecr slp;
          USEVARIABLES ARE smk alc ecr slp;
          CATEGORICAL = smk alc ecr slp; ! 定义分类变量
          CLASSES = c(3); !设定分为3类

ANALYSIS:TYPE = MIXTURE;

OUTPUT:
         TECH11 TECH14;

SAVEDATA: FILE = Prob-MALE-3CLASS.txt;
          Save = cprob;

所得到的Prob-MALE-3CLASS.txt，打开如下所示，红框框出的部分即为分类结果，如下图所示。

6 尾声

以上是LCA分析的结果。总体而言，LCA的作用，是基于多个二分类变量的特征，将人群聚为N类。聚类的过程，首先是通过比较模型系数选定最佳聚类（如本例中，聚为3类是最佳结果）；然后通过概率分布对各类的特点进行定义；最后可以引入分类的结果，做进一步分析。需要注意的是，LCA的分析过程需要反复比较，是通过先验和后验结合不断推敲的过程。

在学习的过程中，除了学习相关文献，数据分析还参考了以下资料：
1. 王孟成、毕向阳所著的《潜变量建模与MPLUS应用:进阶篇》
2. 潜类别分析(Latent Class Analysis, LCA)与Mplus应用(含潜剖面分析, Latent Profile Analysis, LPA)
3. LATENT CLASS ANALYSIS | MPLUS DATA ANALYSIS EXAMPLES

参考文献：
[1] 唐雨蓉,韩茜宇,唐思雨,崔小倩,樊凯盛,宁宁,郝艳华. 2021.新冠疫情下公众应对行为潜在类别分析.中国公共卫生,37(7),1090-1095.
[2] Berger, N., Cummins, S., Allen, A., Smith, R. D., & Cornelsen, L. (2020). Patterns of beverage purchases amongst British households: A latent class analysis. PLoS medicine, 17(9), e1003245.
[3] Cook, W. K., Kerr, W. C., Karriker-Jaffe, K. J., Li, L., Lui, C. K., & Greenfield, T. K. (2020). Racial/ethnic variations in clustered risk behaviors in the US. American journal of preventive medicine, 58(1), e21-e29.

小白的学习笔记